Antoine- oder August-Gleichung, die Clausius-Clapeyron-Gleichung, das Raoult’sche und das Henry-Gesetz – während es relativ aufwändig und gelegentlich unmöglich ist, den Dampfdruck einer Flüssigkeit, einer Lösung oder einer Mischung thermodynamisch exakt zu berechnen, gibt es zahlreiche Näherungsrechnungen für verschiedene Fälle.
Dieser Beitrag soll ein wenig Durchblick durch das Chaos bringen mit
- Teil 1 – Dampfdrücke von reinen Flüssigkeiten
- Teil 2 – Dampfdrücke von Lösungen und Gemischen
Anwendungen
Dampfdrücke von reinen Flüssigkeiten werden benötigt, um die Beladung eines Gasphase oberhalb einer reinen Flüssigkeit zu berechnen, z. B. einem Tank.
Grundlagen
Die Clausius-Clapeyron-Gleichung beschreibt den Verlauf der Siedekurve einer reinen Substanz, d. h. der Grenzkurve zwischen dem Tripelpunkt und dem kritischen Punkt im Phasendiagramm. Deswegen ist sie außerhalb dieser Bereiche auch nicht gültig. Die thermodynamisch exakte Form der Gleichung lautet:
dP/dT = ΔHν/(ΔVν . T)
Um die Steigung der Siedekurve an jedem Punkt bestimmen zu können, braucht man
(a) die druck- und temperaturabhängigen Molvolumina der beiden Phasen und
(b) die druck- und temperaturabhängige molare Verdampfungsenthalpie. Damit es einfacher wird, nimmt man die folgenden Vereinfachungen vor:
- man nimmt an, dass die Verdampfungsenthalpie über den betrachteten Temperaturbereich konstant ist
- man vernachlässigt das Volumen der flüssigen Phase, da sie sehr klein ist gegenüber dem Volumen der Gasphase
- und damit das alles nicht zu genau wird, geht man noch davon aus, dass die Gasphase ein ideales Gas sei, für das gilt: Vm(g) * p = R * T
Dadurch ergibt sich für den Sättigungsdampfdruck nach Integration
ln p = – (ΔHν/(R * T)) + C
Da man die Verdampfungsenthalpie als konstant betrachtet, R eine Konstante und C eine unbekannte Konstante ist, bleibt der Zusammenhang
ln p ~ 1/T
Dampfdruckkurven generieren
Hierzu gibt es grundsätzlich zwei Möglichkeiten, je nachdem, ob man zwei Dampfdrücke bei verschiedenen Temperaturen kennt oder aber die Verdampfungsenthalpie und einen Dampfdruck.
Ist die Verdampfungsenthalpie bekannt, kann man vom Dampfdruck p1 bei T1 auf den Dampfdruck p2 bei T2 schließen:
ln (p1/p2) = (ΔHν/R) * ((T1 – T2)/(T1 * T2))
Wie man mittels einer Tabellenkalkulation eine Dampfdruckkurve aus zwei Punkten konstruiert, wird im folgenden Dokument erklärt: VOC-Rechnen. Eine vorgefertigte Tabelle für Excel bzw. OpenOffice Calc bietet Dr. Heiner Grimm auf seiner privaten Freeware-Seite (weit unten auf der Seite). In die Tabelle braucht man die bekannten Dampfdrücke nur einzusetzen, etwa einen bekannten Punkt und den Siedepunkt mit p = 101.300 Pa.
Die Antoine-Gleichung
Beide Berechnungsmethoden auf Basis der Clausius-Clapeyron-Gleichung sind im Grunde gleich und kranken daran, dass ein linearer Zusammenhang zwischen ln p und 1/T angenommen wird. Die Genauigkeit ist plus-minus einige Prozent, was meistens genügen wird, gelegentlich aber auch nicht.
Die Antoine-Gleichung ist ein Fit mit drei Parametern, der besonders dann angewendet wird, wenn die Clausius-Clapeyron-Gleichung bei höheren Drücken und Temperaturen zu ungenau wird, und hat die Form
log P = A – B/(T + C)
Beim Suchen nach Antoine-Konstanten sollte man aufpassen, auf welche Einheiten und welche Basis des Logarithmus sie sich beziehen. Dies wird leider nicht einheitlich gehandhabt.
Antoine-Koeffizienten finden sich z. B. im NIST Chemistry Webbook. Daten satt gibt es auch im CRC Handbook of Chemistry and Physics (mittlerweile in der 101. Ausgabe angekommen), bzw. in der kostenpflichtigen Online-Version.
Zum Abschluss ist hier noch einmal ein Vergleich der Dampfdruckkurven von Wasser, einmal mit dem o. g. Clausius-Clapeyron-Tool erstellt, einmal mittels der Antoine-Gleichung (Koeffizienten vom NIST Webbook) und die gemessenen Daten aus dem CRC-Handbook. Die Übereinstimmung ist so gut, dass die Grafik sehr groß werden musste, um die minimalen Unterschiede zu zeigen. Wer ein besseres „schlechtes“ Beispiel kennt, möge es doch bitte posten.
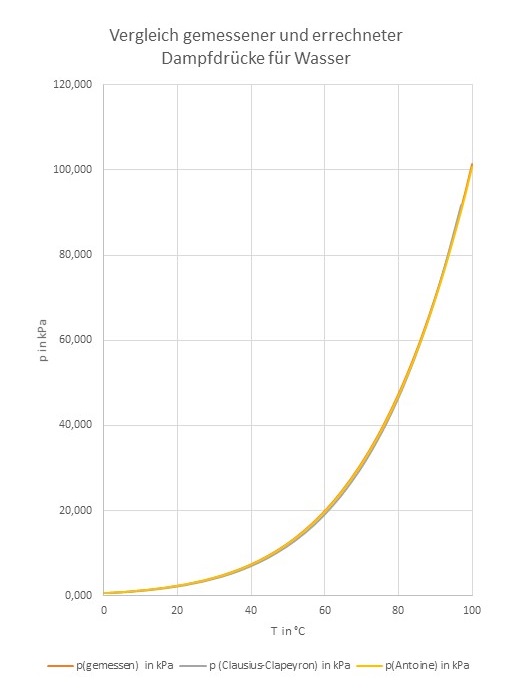
Vergleich der gemessenen Dampfdruckkurve von Wasser mit Ergebnissen der Formeln nach Claudisus-Clapeyron und Antoine
Teil 2 im Juli behandelt die Berechnung von Mischungs- und Lösungsdampfdrücken.
Turner meint
in ln p = – (ΔHν/(R * T)) + C
haben ln p und C die Einheit [ln bar] oder [ln kPa] oder Ähnliches.
Hingegen ist – (ΔHν/(R * T)) dimensionslos, daher nicht wirklich summierbar.
Wo ist der Haken?
Claudia Arnold meint
Vielen Dank für das aufmerksame Lesen! Nach mathematischer Konvention hat ein Logarithmus allerdings nie eine Einheit, erst die entlogarithmierte Form {e^(ln p)} hat wieder einen. So hat auch der pH keine Einheit, er ist nicht „log C“ oder so etwas.
Heiner Grimm meint
Hallo Frau Arnold,
gerade schaue ich mal wieder im Web herum, wo meine Seiten denn überall zitiert werden, und bin nun auf Ihre gestoßen, und diese Diskussion.
Also, der log selbst hat keine Einheit, so weit so richtig, hinzuzufügen wäre, dass sinnvollerweise auch nur reine Zahlenwerte logarithmiert werden können. In
ln (p1/p2) = (ΔHν/R) * ((T1 – T2)/(T1 * T2))
z.B. ist das dadurch gegeben, dass der Quotient aus einem Druck und einem Vergleichsdruck logarithmiert wird. Ein Ausdruck wie ln(p) geht streng genommen gar nicht, korrekt wäre das Logarithmieren des Druckes p, dividiert durch seine Einheit Pa:
ln(p/Pa) = …..
Der pH-Wert ist dimensionslos, und exakt definiert als:
pH = – log10(C/(mol/L)),
wobei das Dividieren durch die Einheit mol/L meist weggelassen wird, warum auch immer.
P.S.: Warum ich als Logo damals ein Alkoholmolekül gewählt hatte? Ich bin selbst nicht sicher, vermute aber mal, ich fand das Molekül gerade komplex genug, ohne bereits unübersichtlich zu erscheinen, und außerdem für Viele irgendwie zum menschlichen Alltag gehörend. (Als Chemiker musste ich natürlich unbedingt ein Molekül nehmen. Als Konsument mag ich Ethanol eher nicht, außer einem Likörchen 1-2 mal im Monat tut sich da nichts. Dagegen verbrenne ich Ethanol oder Methanol gerne mal im Campingkocher. Für das neue, smartphonegerechtere Design habe ich auch vorerst gar kein Logo mehr.)
Freundliche Grüße
Heiner Grimm
Klemeyer meint
Liebe Frau Arnold,
im Rahmen der Gefährdungsbeurteilung nach der TRGS600 bzw. dem GHS-Spaltenmodell zur Substitution wäre es vorteilhat, die Antoine-Koeffizienten für den Dampfdruck von gefährlichen Gasen aus wässrigen Lösungen zur Verfügung stehen würden..
Von besonderem Interesse wären dabei:
HCl (aq); c = 5%, 10%, 25% und 37%
ClO2 (aq); c = 0,3%, 1% und 2%
NaOCl (aq); c = 5% und 10%
Cl2 (aq) c = 0,02 m/l
Br2 (aq) sat.
NH3 (aq); c = 5%, 10%, 20% und 30%
SO2 (aq), c = 6%
Leider habe ich den zweiten Teil noch nicht gefunden. Können Sie mir da weiter helfen?
Claudia Arnold meint
Hallo, Herr/Frau Klemeyer,
der zweite Teil ist hier: http://www.arnold-chemie.de/2008/09/den-dampfdruck-berechnen-teil-2-mischungen-und-losungen/. Allerdings Haben Sie teilweise Verbindungen genannt, die stark solvolysieren, etwa HCl, solche, die in Wasser teilweise zu anderen Verbindungen zerfallen, etwa ClO2, und Salze, die als solche nicht flüchtig sind, erst ihre Zerfalls- und Reaktionsprodukte (etwa NaOCl). Solche Verbindungen lassen sich überhaupt nicht mit dem einfachen Konzept der Antoine-Gleichung abbilden. Schreiben Sie mir doch einfach direkt, z. B. über das Kontaktformular (Link ist oben auf der Seite).
Beste Grüße, Claudia Arnold
Albert Hochmair meint
Danke für die tolle Seite !
Ich möchte eine Flaschenrakete mit flüsssigen Stickstoff ( LN2 )bauen , der Stickstoff ist auf – 192c gekühlt . Der Behälter hat 25l und ist mit ca 20l Wasser mit ca 20c Wassertemperatur gefüllt . Wenn ich da 100ml flüssigen Stickstoff einfülle und die Flasche schnell umdrehe fliegt der Behälter gut 30m hoch in die Luft . Wie viel Energie wird da freigesetzt ? Bzw , wieviel Kwh ? 0
Oder wieviel LN2 brauche ich das das Ding 100m hoch fliegt ?
Besten Dank für ihre Antwort .
https://youtu.be/ANGO-gwLV5E
Claudia Arnold meint
Guten Tag, Herr Hochmair,
diese Frage traue ich mir nicht wirklich zu zu beantworten. Von der Aerodynamik eines umgedrehten Kessels habe ich keine Ahnung, auch nicht davon, wie viel Stickstoff bei diesem spezifischen Behälter ungenutzt verpufft. Im Grunde wird ja keine Energie freigesetzt, sondern Energie der Umgebung (Wasser und Behälter) entzogen, und die ist im einfachsten Fall die Verdampfungsenthalpie von flüssigem Stickstoff bei 20 °C. Derlei Werte kann man sich aus Tabellenwerken wie dem NIST Chemistry Webbook (ist online) heraussuchen. Nun muss das expandierende Gas Verdrängungsarbeit leisten, und das ist stark von den Formfaktoren des Behälters abhängig.
Und dann hoffe ich, dass dieser 25-l-Kessel bei seinem Abstieg niemanden erschlägt!
Beste Grüße, Claudia Arnold