Im ersten Teil dieses Beitrages haben wir einen sehr variablen und schwer nachzumessenden Einflussfaktor auf den Druckverlust betrachtet, nämlich die Porosität ε. „Epsilon“ ε geht in die Ergun-Gleichung mehrfach ein, und kleine Fehler haben große Auswirkungen auf den berechneten Druckverlust. In der Praxis ist die Leerfraktion oder Porosität kaum direkt zu bestimmen:
- Die Porosität ergibt sich aus der Differenz der scheinbaren Korndichte und der Schüttdichte des Bettes. Die Schüttdichte im Adsorber selbst zu bestimmen ist so gut wie unmöglich – welcher Adsorber steht schon auf einer Waage? – und die identische Schüttdichte in einem kleineren Behälter bei nur „ähnlicher“ Befüllungsmethode nachzumessen ist zumindest recht ungenau.
- Die scheinbare Korndichte – also die Dichte der Pellets selbst, einschließlich ihres Porensystems – kann pyknometrisch nachgemessen werden, man benötigt dazu aber Quecksilber statt Wasser. Quecksilber dringt in das Porensystem, im Gegensatz zu Wasser, nämlich nicht ein. Das Hantieren mit solchen Mengen flüssigen Quecksilbers ist nicht empfehlenswert, und die meisten Anwender würden vermutlich auch auf Beschaffungsprobleme stoßen.
Indirekt könnte man die Porosität eines gegebenen Bettes natürlich aus den Druckverlustkurven bestimmen, indem man ε fittet. Dafür muss man jedoch den Druckverlust selbst messen.
Ergebnisse auf Basis von Literaturwerten
Für Zwecke der Abluftbehandlung mit Zeolithen eignet sich nur die Ergun-Gleichung für die Berechnung von Druckverlusten, weil man sich dort meist im Übergangsbereich der Strömung – mit Reynolds-Zahlen zwischen 0,5 und 1.000 – bewegt. Bei einer Porosität von ε = 0,44, Partikeln von d = 1,5 mm und einer Leerrohrgeschwindigkeit von s = 0,1 m/s liegt die Partikelreynoldszahl bei Re = 22,0, bei s = 0,9 m/s bei Re = 200 (trockene Luft bei 20 °C).
Ich habe nun Herstellerangaben von Druckverlusten mit Rechenergebnissen verglichen – mit durchweg mäßigen Ergebnissen.
1 – 3 mm große Perlen
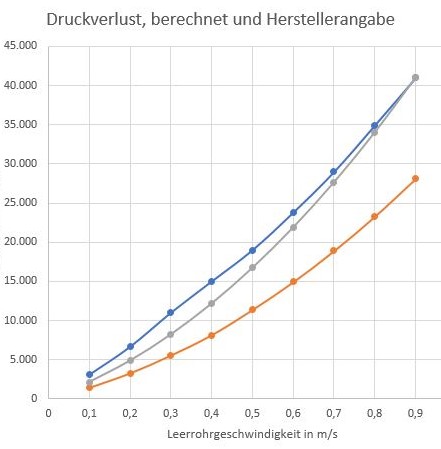
Vergleich von gemessenem und Berechneten Druckverlust, trockene Luft bei 20 °C. Blau: Druckverlustangaben des Herstellers. Orange: berechnet mit einer Porosität von 0,350. Grau: Berechnet mit einer Porosität von 0,315.
Die blaue Kurve gibt die Herstellerangaben für den Druckverlust der Partikelfraktion 1 – 2 mm wider. Hier war schon die erste Schwierigkeit zu überwinden: Welchen Partikeldurchmesser einsetzen? Ich habe einen Mittelwert von 1,5 mm angenommen. Zwar gibt es Literaturwerte [1] darüber, welche Porositäten in Schüttungen zu erwarten sind, abhängig von Faktoren wie Behälterdurchmesser, Einfüllmethode, Oberfläche der Partikel etc. – aber alle Messungen wurden mit gleich großen, perfekten Kugeln durchgeführt, die eigens für den Versuch angefertigt wurden. Anhand der Literatur würde ich eine Porosität von ε = 0,350 erwarten (orangefarbene Kurve) – und liege mit der Druckverlustberechnung mehr als nur haarscharf daneben.
Wenn ich eine Porosität von ε = 0,315 annehme (volle 10% dichter!), kommt der Druckverlust schon besser hin. Ungleich große Kugeln scheinen zu einer besseren Raumerfüllung zu führen, welche nicht berechnet werden kann (zumindest nicht mit Laienmitteln). Auch fällt der etwas andere Verlauf der Kurve in der unteren Hälfte auf, die nur teilweise auf Ablesefehler zurückzuführen ist. Die anderen Gründe können nicht nachvollzogen werden: Wurde der Behälter zwischenzeitlich bewegt? Für andere Versuche verwendet, die zu einem Setzen der Schüttung führten?
Eine errechnete und gemessene Druckverlustkurve sind so nicht zur Deckung zu bringen. Höchstens kann man eine derart errechnete Druckverlustkurve, die auf Basis eines Fits an vorhandene Werte gewonnen wurde, benutzen, um leichter an einzelne Zwischenwerte zu kommen.
Porosität und Druckverlust
Trägt man für einen bestimmten Strömungszustand (hier für s = 0,4 m/s, ansonsten alle Bedingungen wie oben) den Druckverlust nach Ergun gegen die Porosität auf, bekommt man einen Eindruck davon, wie einflussreich die Porosität ε ist.
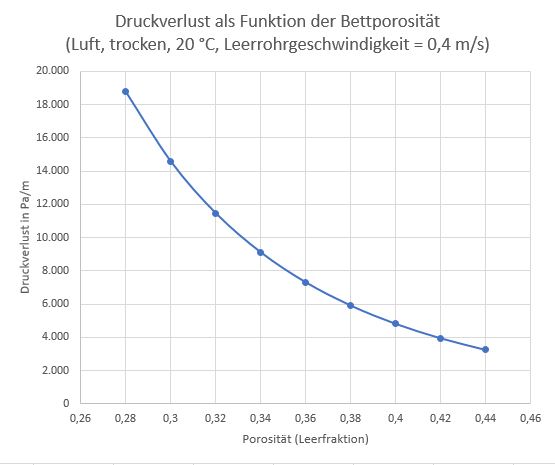
Druckverlust als Funktion der Porosität: 1 – 2 mm Perlen, trockene Luft bei 20 °C, Leerrohrgeschwindigkeit s = 0,4 m/s.
Man stelle sich vor: Ein paar mal gegen den Behälter geklopft, und der Druckverlust steigt um 2.000 Pa/m? Das ist durchaus drin, wenn eine langsam eingeschüttete Adsorbensmasse durch Rütteln verdichtet wird. Die Schüttung kann sich natürlich auch durch thermisches Ausdehnen und Zusammenziehen im Laufe des Ad- und Desorptionsbetriebes verdichten. Als Betreiber könnte man auf die Idee kommen, die Schüttung habe sich mit Fremdstoffen zugesetzt, dabei hat sie sich nur in sich gesetzt. [2]
Wenn es keine Kugeln sind…
Adsorbenzien gibt es in sehr verschiedenen Formen. Wenn man statt Kugeln Stäbchen, „Makkaroni“ oder Kleeblätter vor sich hat, gibt es gleich zwei unbekannte Parameter, die man in die Ergun-Gleichung einsetzen muss: Die Porosität ε und den äquivalenten Korndurchmesser dST. Letzterer ist der Durchmesser einer Kugel mit einem Durchmesser, die die gleiche Auswirkung auf den Druckverlust hat wie das nicht-kugelförmige Korn. dST hängt von der Position der Körner in der Schüttung ab – liegen sie, oder stehen sie eher? – und ändert sich mit der Porosität. Spätestens ab hier gerät jeder Berechnungsversuch zu reiner Zahlenspielerei.
Um gemessene Druckverluste führt, wie es aussieht, nun einmal kein Weg herum.
[1] Z. B. in Ribeiro, A. M., Neto, P., & Pinho, C. (2010). Mean Porosity and Pressure Drop Measurements in Packed Beds of Monosized Spheres: Side Wall Effect. International Review of Chemical Engineering, 2(1), 40–46.
[2] Besonders hinterhältig: Bei quer durchströmten Behältern kann sich auf diese Weise oben ein ganz ordentlicher Kanal ausbilden.
Schreibe einen Kommentar