Ursprünglich sollte dieser Artikel heißen „Über die Randgängigkeit von Schüttungen“. Ich wollte darin der Frage nachgehen, ob die oft zitierte Behauptung, ein Schüttbett müsse für gleichmäßige Durchströmung wenigstens zehn Partikeldurchmesser als Durchmesser haben, irgendeine Grundlage hat. Diese Grundlage gibt es tatsächlich, aber die Frage ist nur eine Variation der größeren Frage nach der Schüttdichte, und somit dem Druckverlust eines Schüttbettes.
Die Randgängigkeit
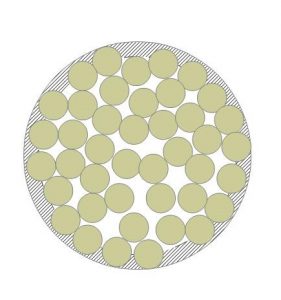
Randzone einer Schüttung (schraffiert)
Randgängigkeit bedeutet, der Druckverlust eines Fluids ist entlang der Kolonnenwand bei gleicher Leerrohrgeschwindigkeit geringer als in der Mitte der Schüttung. In der Abbildung ist das der schraffierte Bereich, einen halben Partikeldurchmesser breit. Zwar verursacht die Wand Reibung und erhöht den Druckverlust, das kann aber durch die geringere Schüttdichte der Partikel in dieser Zone mehr als ausgeglichen werden. Die Strömung teilt sich in eine Rand- und eine Bulkströmung auf, der Druckverlust ist in beiden Zweigen gleich, weil der Volumenstrom sich natürlich entsprechend ausbalanciert.
Bei größeren Schüttbetten ist dieser Effekt unmerklich, aber unter ungünstigen Bedingungen – zu kleinen Kolonnen und weiteren Faktoren, die den störenden Einfluss der Wand stark werden lassen – erhält man einen geringeren Druckverlust als erwartet, und im schlimmsten Fall einen sofortigen partiellen Durchbruch.
Wovon hängt der Druckverlust ab?
Von allen Faktoren, die den Druckverlust durch eine Schüttung bestimmen, sind nur wenige einigermaßen leicht zu bestimmen. Die Einflussfaktoren sind im Folgenden
- Geometrisch:
- Die Betthöhe hat einen Einfluss durch Ein- und Austrittseffekte, welche bei ausreichend tiefer Schüttung verschwinden
- Das Verhältnis von Partikelgröße zu Behälterdurchmesser, weil es die Schüttdichte beeinflusst
- Die Art der Partikel:
- Ihre Form – mehr oder weniger rund bis hin zu schuppen- oder plättchenförmig
- Ihre Orientierung (es zählt am Ende die der Strömung zugewandte Fläche)
- Ihre Oberflächenbeschaffenheit, also rau oder glatt
- Die Dichte des Materials – Stahl- oder Kunststoffkugeln verhalten sich unterschiedlich.
- Die Porosität der Schüttung, also der für das Fluid verbleibende Raum
- Die Partikel-Reynoldszahl, die sich nur indirekt bestimmen lässt, da hierfür die Geschwindigkeit des Fluids direkt am Korn bekannt sein muss, die Leerrohrgeschwindigkeit hilft einem nicht weiter. Die Fluidgeschwindigkeit ist, bedingt durch die Engstellen in einer Schüttung, lokal stark unterschiedlich.
Es gibt neben der bekannten Ergun-Gleichung zahlreiche andere Ansätze zur Berechnung des Druckverlustes in einer Schüttung. Eine Zusammenstellung von zehn verschiedenen Ansätzen liefert z. B. das Skript vom Institut für Verfahrenstechnik der Otto-von-Guericke-Universität Magdebunrg (ab Folie 4.15). Heute soll es nur um einen dieser Einflussfaktoren gehen, nämlich die Porosität.
Weit weg von der dichtesten Kugelpackung
Die dichteste Kugelpackung, die in zwei Varianten existiert, lässt zwischen den Kugeln noch 26% Leerraum, hat also eine Porosität ε von 0,26 und eine unendliche Fernordnung. Diese bildet sich beim Einschütten realer Materialien in einen Behälter jedoch nicht aus, tatsächliche Porositäten liegen 0,44 und 0,359 für Schüttungen aus Kugeln.
Porositäten von Kugelpackungen
| Typ | Porosität, ca. | Entstehung |
|---|---|---|
| Ultralose | 0,44 | Sedimentation oder langsames Herunterfahren eines fluidisierten Bettes |
| Lose | 0,4 - 0,41 | Kugel für Kugel wird nacheinander eingerollt |
| Geschüttet | 0,375 - 0,391 | Einschütten der Kugeln in den Behälter |
| Dicht | 0,359 - 0,375 | Nach dem Einschütten gerüttelte Packung |
| Dichtest | 0,26 | Ideale dichteste Kugelpackung |
Kleine Abweichungen der Schüttdichte verursachen einen großen Fehler bei der Berechnung des Druckverlustes, z. B. bei Anwendung der Ergun-Gleichung. ε geht darin ein als (ε² – 2ε+1)/ε³ + (1 – ε)/ε³. Der Zusammenhang wurde in der folgenden Abbildung geplottet (alle anderen Variablen und Konstanten wurden als 1 gesetzt, weswegen das Ergebnis, das sich auf keinen konkreten Fall bezieht, dimensionslos ist). Man erkennt daran, dass in dem Bereich der Porosität, der für Kugelpackungen gilt, ein Fehler von 1% bei der Angabe der Porosität zu einem Fehler von ±5% beim errechneten Wert für den Druckverlust führt [2].
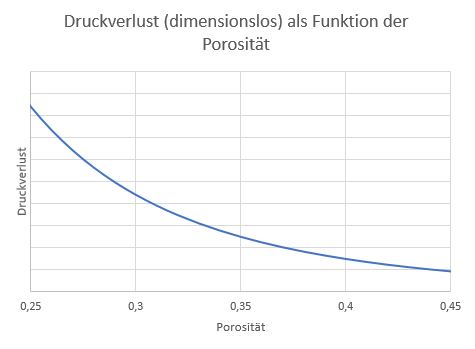
Dimensionsloses Maß für den Druckverlust aufgetragen gegen die Porosität ε.
Auswirkung des Behälterdurchmessers
Je enger ein Rohr ist, desto weniger können die darin eingeschütteten Partikel einander seitlich ausweichen und sich in einem lokalen Minimum potenzieller Energie festsetzen – das ist intuitiv vorstellbar. Was sagen die Messungen? Die folgende Abbildung stammt aus [2].
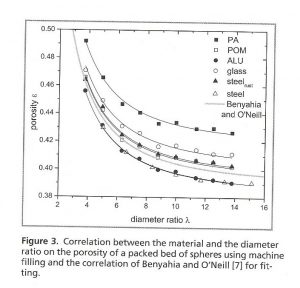
Schüttdichte als Funktion des Verhältnisses von Partikel- zu Behälterdurchmesser, für verschiedene Materialien, aus [2] (Klick für größere Version)
Im nächsten Beitrag wollen wir uns einige konkrete Rechenmethoden für den Druckverlust anschauen und sehen, wie sie im Vergleich zu den Druckverlustkurven, welche von Herstellern herausgegeben werden, abschneiden.
[1] Ribeiro, A. M., Neto, P., & Pinho, C. (2010). Mean Porosity and Pressure Drop Measurements in Packed Beds of Monosized Spheres: Side Wall Effect. International Review of Chemical Engineering, 2(1), 40–46.
[2] Pottbäcker, J., & Hinrichsen, O. (2017). Experimental Study on the Influence of Filling Method and Particle Material on the Packed-Bed Porosity. Chemie-Ingenieur-Technik, 89(4), 454–458. http://doi.org/10.1002/cite.201600151
Schreibe einen Kommentar