
… oder „Über den Sinn und Unsinn von Nachkommastellen“.
Luft kann, je nach Druck und Temperatur, recht unterschiedliche Dichten annehmen, das lehrt schon der Augenschein. Gerechnet wird im Abluft- und Klimabereich jedoch mit den pauschalen 1,2 kg/m³ – und sagte nicht schon Gauss: „Durch Nichts gibt sich mathematische Unbildung so zu erkennen wie durch maßlose Schärfe im Zahlenrechnen“? Wie genau muss die Dichte sein?
Ideales Gasgesetz
Am einfachsten werden Gasdichten durch das Ideale Gasgesetz berechnet, nach dem die Dichte eines (nicht allzu komprimierten und im Idealfall überkritischen) Gases gegeben ist durch: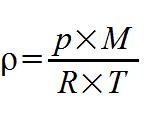
mit dem Druck p, der molaren Masse des Gases in kg/mol, der Universellen Gaskonstante R und der Temperatur in Kelvin. Die Einheit der Dichte ist kg/m³. Nun ist Luft aber eine Mischung aus Stickstoff und Sauerstoff, etwas Argon (Kohlendioxid sollte nur in Spuren da sein) und Wasserdampf. Die Menge des letzten wechselt sehr stark, und Wasserdampf bei atmosphärischen Bedingungen ist bei weitem nicht überkritisch. Was tun?
Angepasste Gaskonstanten
In der Praxis rechnet man mit einer angepassten Gaskonstante für feuchte Luft, die massen-, und nicht molbasiert ist. Diese wiederum errechnet sich aus der Gaskonstante für trockene Luft, der für Wasserdampf, dem Umgebungsdruck und dem Dampfdruck des Wassers bei Umgebungstemperatur. Dann kann weitergerechnet werden wie oben. Die private Website von Anton Schweizer enthält z. B. eine ausführliche Formelsammlung zum Thema, Wikipedia einen einführenden Artikel und von dort aus verlinkt wird der grandiose Rechner von Hygrothermik, ebenfalls eine private Website.
Ich biete für die Bestimmung der exakten Luftdichte ein Excel-Sheet „Exakte-Luftdichte“ an, das Sie herunterladen können. Der Wasserdampfdruck sollte idealerweise aus Tabellenwerken stammen, zur Not sind aber die Dampfdrücke aus der Antoine-Gleichung hinterlegt.
Und wie sehr schwankt nun die Dichte der Luft?
Beispiel 1: Sommer und Winter
Die Dichte der Luft bei 35 °C, 65% relativer Feuchte und Normaldruck beträgt 1,129 kg/m³, bei 0 °C, 15% r.F. und Normaldruck dagegen 1,292 kg/m³ – eine Erhöhung um gut 14%. Sogar Herr Gauss hätte nichts gegen diese Unterscheidung einzuwenden gehabt.
Beispiel 2: Dschungel und Sahara
Im Dschungel (35 °C, 90% r. F. und 980 hPa [1]) hat die Luft eine Dichte von 1,08 kg/m³, in der Sahara mit ebenfalls 35 °C, aber nur 20% relativer Feuchte und einem Luftdruck von 1020 hPa beträgt die Dichte 1,148 kg/m³. Das ist ein Unterschied von 5,7%.
Die vielzitierten 1,2 kg/m³ …
… liegen vor bei mittleren Bedingungen – 20 °C, 50% relativer Feuchte und Normaldruck (1013 hPa). Und im Inneren des Heißluftballons? Das hängt vom Wetter ab – je wärmer, desto mehr muss die Luft in der Ballonhülle erhitzt werden, damit der Auftrieb ausreicht: Im Winter reichen 50 – 60 °C, im Sommer werden fast 100 °C benötigt – weswegen eine Ballonfahrt im Sommer mit gleicher Gasflasche nicht so lange dauert. [2]
[1] Persistente Tiefdrucklagen sind charakteristisch für die tropischen Regengebiete der Erde. Ebenso haben die Wüstenzonen auf Höhe der Wendekreise eher einen hohen Luftdruck, ebenso wie die Polargebiete.
[2] So erklärt auf der FAQ-Seite eines gewerblichen Anbieters von Ballonfahrten: Ballonfahrt-Team Mettingen.
Gast meint
Hallo Frau Dr. Arnold,
in der Gleichung zum idealen Gas fehlt leider eine Klammer.
die Gleichung heisst eigentlich: ρ = p * M/(R * T)
Grüße
Jürgen Michele meint
https://www.arnold-chemie.de/2016/02/die-genaue-dichte-von-feuchter-luft-berechnen/
Die Einheit der Dichte ist kg/m³. Nun ist Luft aber eine Mischung aus Stickstoff und Sauerstoff, etwas Argon (Kohlendioxid sollte nur in Spuren da sein) und Wasserdampf. Die Menge des letzten wechselt sehr stark, und Wasserdampf bei atmosphärischen Bedingungen ist bei weitem nicht überkritisch. Was tun?
Der Wassergehalt in der Atmosphäre ist entscheidend für die Konvektion – wegen des Wassergehaltes.
Den meisten Menschen und auch vielen Meteorologen ist nicht bekannt, dass feuchte Luft leichter ist als trockene – der Grund für das Schweben von Wolken.
Jürgen Michele
Warum schweben Wolken?
Selbst Kinder stellen die Fragen: Warum schweben Wolken? Wie schwer ist eine Wolke?
Diese Fragen sind nicht so leicht zu beantworten.
Im Internet kann man heute verschiedene Antworten finden: Die häufigste Antwort, die man findet ist die, dass die in der Wolke vorhandenen Wassertröpfchen so klein sind, dass diese – wie man an feinen Staubteilchen in der Zimmerluft beobachten kann – in der Luft schweben und von kleinsten Strömungen mitgerissen werden.
Wie groß sind die sichtbaren Wassertröpfchen? Bei Wikipedia findet man:
„Die Tröpfchendurchmesser innerhalb eines Nebels sind mit wenigen hundertstel Millimetern wesentlich geringer als in einer typischen Wolke, durch die unterschiedlichen Kondensationskerne schwanken sie jedoch auch stark zwischen den einzelnen Tropfen. Dabei entscheidet deren Größe, ob ein Nebel nässend ist oder nicht. Ist er leicht nässend, so handelt es sich um eine Tröpfchengröße, die im Mittel 10 bis 20 μm nicht überschreitet, bei dichtem Nebel sind es eher 20 bis 40 μm. In Einzelfällen wurden auch schon Tröpfchengrößen von 100 μm festgestellt, dieses ist aber eine Ausnahmeerscheinung. Kleinere Tropfenradien weisen dabei auf maritime Bedingungen hin, größere Radien hingegen auf kontinentale Verhältnisse. Bei Nebel enthält ein Kubikmeter Luft in Form der Tröpfchen etwa 0,01 bis 0,3 Gramm kondensiertes Wasser.“
Dies gilt auch für Wolken. Wolken sind nichts anderes als nichts anderes als Nebel, allerdings werden sie als solche nur von außerhalb der Nebelzone wahrgenommen. Trotz der sehr großen Tröpfchenzahl (>108/m3) ist die Masse wegen der geringen Durchmessergröße nur so klein. Bei Wolken, die abregnen sind die Tropfen deutlich größer.
Nebel weist eine relative Luftfeuchtigkeit auf, die bei 100% liegt. Es ist wesentlich mehr „unsichtbares“ als „sichtbares“ Wasser in einer Wolke vorhanden! Die normale Luftfeuchtigkeit, das ist also der Gehalt an nicht sichtbarem „kaltem“ Wasserdampf (Wassermoleküle), hat also eine größere Masse als die sichtbaren Tröpfchen.
In einer Quizsendung, in der „Sendung mit der Maus ..“ und auch in einer Sendung von „Kopfball“ wurde versucht, die Frage nach der Masse einer Wolke zu beantworten. Die Abschätzung der Größe ergab, dass die Masse einer größeren Wolke der eines Jumbojets entsprechen würde.
Die Erklärung des Schwebens der Wassertröpfchen und damit der Wolken mit deren geringen Teilchengröße der darin enthaltenen Tröpfchen wird auch von Fachleuten – sogar in wissenschaftlichen Zeitschriften – verbreitet!
Eine solche Aussage ist aber nicht zu halten. Partikel und selbst schwere Moleküle sinken in ruhender Luft ab. Messungen am Stachus in München haben ergeben, dass die Konzentration von CO2 und auch die von anderen schweren Schadstoffmolekülen am Boden und in den dortigen Souterrainwohnungen deutlich höher ist als wenige Meter höher.
Strömungsmechaniker und Verfahrenstechniker können die im Internet und der Literatur zu findenden Begründungen für das Schweben einer Wolke nicht zufrieden stellen.
Vielen wird das klassische Experiment „Cartesischer Taucher“ bekannt sein. Zu finden:
https://philiki.uni-kiel.de/index.php/versuche/versuche-mechanik/275-2012-02-20-134656
oder einfach googlen.
Durch Drückerhöhung wird die Luft im Taucher komprimiert und die „Dichte“ des Tauchers erhöht sich. Er sinkt jetzt ab. Dichte ist die Zauberformel für Schweben. Dies gilt auch für das Schweben einer Wolke. Jeder einzelne auch noch so kleine Tropfen muss von einer Aufwärtsströmung in der Schwebe gehalten werden.
Den meisten Menschen ist die Tatsache nicht bekannt, dass feuchte Luft eine geringere Dichte hat als trockene. Es scheint ja auch mehr als naheliegend, dass wenn Feuchte in die Luft hineinkommt, diese natürlich schwerer werden sollte. Hier spielt die Natur aber anders mit.
Die Dichte ist entscheidend für das Schweben der Wolke. Hier stellt sich die Frage, gibt es Dichteunterschiede für die Luft, wenn Druck und Temperatur gleich sind? Diese Antwort fällt leicht. Natürlich hat die Zusammensetzung der Luft auch einen Einfluss. Hier ist die Luftfeuchtigkeit zu nennen. Ist dieser Einfluss wesentlich?
Wenn man mit den bekannten Gleichungen der Thermodynamik die Luftdichten bestimmt, erhält man z.B. für die Temperatur von 20°C bei „Normaldruck“ Werte für trockene Luft von 1,205 kg/m3 und für 100% relative Luftfeuchtigkeit von 1,194 kg/m3. Das macht einen Unterschied von nur 11 g/m3. Dies erscheint erst einmal als ein so kleiner Wert, der kaum Einfluss haben sollte. Aber wenn man auf die Masse des sichtbaren Wassers in der Wolke von deutlich weniger als 1g/m3 schaut relativiert sich der Sachverhalt.
Wenn man seine Bekannten die Frage nach der Dichte von feuchter Luft stellt, erhält man sehr selten die richtige Antwort. Auch meine Kollegen hatten nicht die richtige Antwort. Nur ein Kollege – ein Chemiker -, der mich besser kannte und wusste – der Michele stellt immer so „dumme“ Fragen – hatte nach kurzem Nachdenken die richtige Antwort.
Warum ist Chemie an dieser Stelle hilfreich? Als die Chemie von der „Allchemie“ zur modernen quantitativen Chemie wurde, hatte Avogadro 1811 gefunden, dass die Zahl der Moleküle in einem Gasvolumen bei konstanten Druck und gleicher Temperatur gleich ist. Loschmidt hat diese Zahl 1865 als erster bestimmt.
Was bedeutet dies für die Dichte von feuchter Luft? Wenn einem Gasvolumen Wasser gasförmig hinzugefügt wird (Beispiel Verdunstung) müssen aus diesem Volumen die schwereren Moleküle Sauerstoff und Stickstoff verschwinden. Damit wird die Dichte geringer!
Welches sind die Folgerungen? Dies ist der entscheidende Grund weshalb Wolken schweben. Aber auch Instabilitäten der Atmosphäre werden durch Dichtunterschiede hervorgerufen.
Eine quasistationäre Wolke hat die gleiche Dichte wie das gleich große Luftvolumen in gleicher Höhe und bei gleicher Temperatur.
Wolken sind nie im Gleichgewicht. Da die Tröpfchen sinken muss der Wolke immer Energie – Wärme oder Bewegungsenergie – zugeführt werden. Wenn dies unterbleibt lösen sich Wolken auf. Nebel „steigt auf“ oder „fällt herunter“.
Auch kleinste Partikel in einem Raum schweben nur, weil geringe Geschwindigkeiten der Luft – hervorgerufen durch geringste Temperaturunterschiede – diese in Schwebe halten.
Nun noch zur Frage nach der Masse einer größeren Wolke. Die Wolkenmasse ergibt sich zu mehr als 90% aus der Luft selbst. Ein wesentlicher Anteil ist das „unsichtbare“ Wasser. Die Masse der sichtbaren Wassertröpfchen macht den kleinsten Anteil aus.
Die Antwort: „Eine Wolke ist schwerer als ein Jumbojet“ ist nur kurios …
Warum schweben Wolken?
Im Internet habe ich wenige vernünftige Antworten gefunden!Zur Dichte von feuchter Luft
Alte Antwort …
Es ist nur wenigen geläufig, dass feuchte Luft eine geringere Dichte hat als trockene …
Selbst manche Meteorologen haben hier Defizite. Sie arbeiten mit “potentiellen Temperaturen”.
In einer Wolke liegt die relative Luftfeuchtigkeit bei 100%.
Clouds are made up of tiny water or ice droplets, depending on temperature. This implies that cloud density is greater than that of dry air. Why don’t clouds sink through their surrounding atmosphere rather than float by in a variety of formations?
https://physics.stackexchange.com/questions/9898/the-density-of-clouds
https://antwortenhier.me/q/Die-dichte-von-wolken-33339848684
Air Density Calculations
Calculations with Vaisala: http://go.vaisala.com/humiditycalculator/5.0/
All calculations at a pressure of 1013.25mbar Temperature 20°C rel. humidity 0%: density: 1.2041 kg/m^3 100% 1.1936 kg/m^3 Density difference: 10.5 g/m^3
Temperature 24°C rel. humidity 0%: density: 1.1879 kg/m^3 100% 1.1747 kg/m^3 Density difference: 13.2 g/m^3
Temperature 30°C rel. humidity 0%: density: 1.1644 kg/m^3 100% 1.1459 kg/m^3 Density difference: 18.5 g/m^3
Temperature 34°C rel. humidity 0%: density: 1.1439 kg/m^3 100% 1.1264 kg/m^3 Density difference: 17.5 g/m^3
At the first glance these differences look quite small. But taking into account that fog holds less than 0.3g of condensed water as micron sized droplets it is very large. The amount of invisible water is much higher in that air. What is the effect of temperature? 20°C vs 24°C: at 0% rel. hum. Density difference: 1.2041 – 1.1879 = 16.2 g/m^3 30°C vs 34°C: at 100% rel. hum. Density difference: 1.1459 – 1.1262 = 19.7 g/m^3
Density differences because of humidity differences are in the same order of magnitude as with temperature differences and will drive instabilities. Humidity is in so far more important as condensation during up rise will release higher air temperature.
Fluid mechanics: Density differences cause pressure differences. These cause fluid motion. Navier – Stokes – Equations do not deal with “potential temperatures” …
Hier mein Kommentar an anderer Stelle.