Warum diffundiert Sauerstoff schneller aus einem Gummireifen als Stickstoff? Warum lässt sich in bestimmten Zeolithen para-Xylol von den anderen Isomeren abtrennen? Ein wichtiger Einflussfaktor, wenn auch nicht die ganze Antwort, liegt im kinetischen Durchmesser der Moleküle.
Für den kinetischen Durchmesser findet man stark abweichende Angaben in verschiedenen Datenquellen, und tatsächlich schwankt der ermittelte Durchmesser nach Art der Bestimmungsmethode. Schließlich gibt es keine Pico-Schieblehre, die man an die Moleküle halten könnte. Und selbst wenn es sie gäbe, so sind Atome und Moleküle keine harten Gebilde, sondern diffus begrenzt, wie von der Elektronenwellendichtefunktion beschrieben.
Je nachdem, ob der effektive Durchmesser der Teilchen dadurch gemessen wird, wieviel Raum sie in einem Kristall oder in einer Flüssigkeit einnehmen, oder welchen Querschitt sie in der Gasphase „abfegen“, können sich unterschiedliche Werte ergeben.
Definition
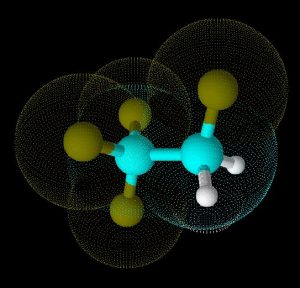
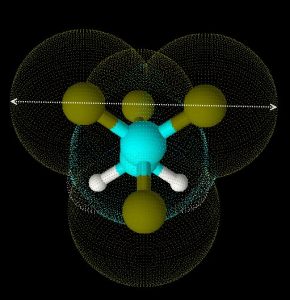
Vereinfacht gesagt ist der kinetische Durchmesser der kleinste Durchmesser, den das Molekül seiner Umgebung präsentieren kann. Die Abbildungen zeigen das Molekül R 134 a (1,1,1,2-Tetrafluorethan, ein Kältemittel) einmal von der Seite, und einmal frontal. Der größte Durchmesser der Frontalansicht entspricht dem kinetischen Durchmesser, in diesem Fall ca. 5,2 Å (520 pm). (Klick auf das Bild führt zur größeren Ansicht – und unter AntiVir leider zu einer Viren-Falschmeldung, die hoffentlich demnächst abgestellt werden wird.)
Dr. Keith Murphy von Air Products and Chemicals, Inc. erläutert in seinem Artikel sehr anschaulich, was der kinetische Durchmesser ist und welche Rolle er bei der Membranpermeation spielt. Die Webseite ist allerdings die eines „Instituts zur Förderung von Stickstoff in Autoreifen“ und somit nicht ganz frei von kommerziellen Interessen.
Verschiedene kinetische Durchmesser?
Das CRC Handbook of Chemistry and Physics nennt drei Arten von Moleküldurchmesser: Errechnet aus Viskositätsdaten, aus der van der Waals’schen Gleichung und aus der Wärmeleitfähigkeit. Es gibt daneben noch weitere Methoden, z. B. kann man die „Maße“ des Moleküls nach dem Baukastenprinzip aus Bindungswinkeln, Bindungslängen und van der Waals-Halbmessern berechnen (lassen). In den meisten Fällen weichen die Daten nur um 2 – 3% voneinander ab, aber es gibt auch Fälle wie den von Helium: Dort beträgt der Unterschied fast 30%. Der kinetische Durchmesser von Helium, berechnet aus der Viskosität, beträgt 190 pm (1,9 Å), berechnet aus der van der Waals’schen Gleichung 2,65 Å.
Der kinetische Durchmesser ist nicht das allentscheidende Kriterium für das Diffusionsverhalten von Molekülen. Andere Eigenschaften wie Molekulargewicht, Polarität, Polarisierbarkeit, Dipolmoment und die statistische Wahrscheinlichkeit einer bestimmten Molekülkonformation spielen ebenfalls eine Rolle. Als einfaches Beispiel seien lineare Kohlenwasserstoffe genannt, also CH3-(CH2)n-CH3. Berechnet man den kinetischen Durchmesser dieser Moleküle nach der grafischen Methode, wie oben beschrieben, ergibt sich immer der selbe Wert, schließlich handelt es sich um molekulare „Würmer“ unterschiedlicher Länge, aber gleicher Dicke. Zwar neigen die Kohlenwasserstoffmoleküle mit zunehmender Länge verstärkt zur Knäuelbildung, sie können sich aber auch ausstrecken und in Zeolithporen eindringen. Hierbei sind längere Moleküle allerdings um viele Größenordungen langsamer als kürzere.
Der kinetische Durchmesser ist aber ein Ausschlusskriterium, wenn es um die Adsorption in oder Diffusion durch mikroporöse Stoffe mit definierter Porengröße geht. Was (bei der gegebenen Temperatur) zu groß ist, geht eben nicht hinein. Wie schnell das Molekül aber hineingeht, wenn es klein genug ist, hängt von vielen Faktoren ab.
Das tragbare Loch –
– oder warum Zeolithporen manchmal funktional größer sind als sich nach kristallographischen Daten berechnen lässt: Erst am thermodynamischen Nullpunkt, also bei – 273,15 °C, wäre ein Zeolithgitter so starr und still, wie die Baukastenmodelle es suggerieren. Bei höheren Temperaturen schwingt es, kann deformiert werden (wie die eindringenden Moleküle auch), so dass sich manchmal scheinbare Abweichungen von über 1 Å ergeben. Zudem können Berechnungen von Porenöffnungen auch unterschiedliche Werte ergeben, je nachdem welche van der Waals-Durchmesser man ansetzt. Sehr anschaulich wird das erklärt im Kapitel 5. 1. 2. des Buches „Molecular Transport and Reaction in Zeolites“ von N. Y. Chen et al.
Bestimmung des kinetischen Durchmessers aus der Viskosität von Gasen
Die Firma Phywe Systeme, ein Anbieter von Lehrmitteln für die Naturwissenschaft, erklärt in einem Beiblatt zum Versuchsaufbau, wie die Bestimmung des Moleküldurchmessers durchgeführt wird.
Aus der van-der-Waals-Gleichung für reale Gase
Der Hintergrund wird knapp in Band II von „Atome – Moleküle – Kerne“ von Otter und Honecker erklärt, einzusehen auf Seite 8 der Google-Buchvorschau. Während die ideale Gasgleichung davon ausgehen, dass die Teilchen eines Gases keinen Raum einnehmen (was angesichts der geringen Dichte eines Gases auch näherungsweise stimmt), führt die van-der-Waals-Gleichung für reale Gase ein Kovolumen b als Korrekturterm ein. (Van-der-Waals-Koeffizienten sind nicht so leicht zu finden, aber einige Links in dem mittlerweile drei Jahre alten Newsletter zum Thema sind noch aktuell.)
Baukastenmethode
Mit Hilfe von ChemSketch habe ich für einige Moleküle den kinetischen Durchmesser bestimmt und mit Literaturwerten verglichen. Zwar gibt es keinen immergültigen Wert für den kinetischen Durchmesser, sondern nur den besten Wert für einen bestimmten Anwendungsfall. Man kann aber aus dem Vergleich wenigstens sehen, wie gut die mit einer Freeware erstellten Werte im Vergleich zu aufwändiger bestimmten Werten abschneiden.
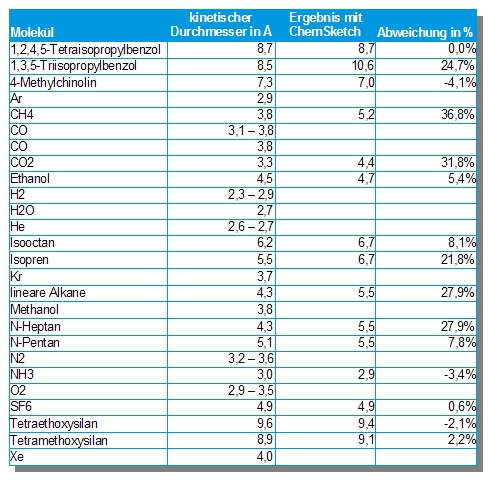
Tabelle kinetischer Durchmesser von Molekülen und Edelgasen
Wie die Berechnung funktioniert, wird in Blogeintrag „Kostenlose Datenbanken …“ erklärt, unter dem Stichwort „Size matters – es kommt eben doch auf die Größe an“.
Schreibe einen Kommentar