Monte-Carlo-Simulation für Arme, Teil I

Monte-Carlo – das klingt zunächst mehr nach Glücksspiel als nach Mathematik. Tatsächlich hat die Monte-Carlo-Simulation ihren Namen von dem für seine Spielbanken bekannten Ort am Mittelmeer. Es ist eine in den 40er Jahren entwickelte Technik der Vorhersage oder Risikoanalyse mit stochastischen Mitteln.

Auch als Alternative zur analytischen Lösung mathematischer Probleme kann die Methode eingesetzt werden, man bekommt dann eine Annäherung. Wie es funktioniert, zeigt beispielhaft die Abschätzung der Zahl π.

In ein Quadrat wird ein Viertelkreis eingezogen. Dann wird willkürlich verteilt auf das Quadrat „geschossen“ (d. h. es werden zufällige Koordinatenpaare generiert) und jeweils entschieden, ob der Punkt innerhalb oder außerhalb des Kreises liegt. Diese Entscheidung kann mit dem Satz von Pythagoras getroffen werden, man braucht dafür π also nicht. Das Verhältnis der Anzahl der Punkte im Viertelkreis zur Gesamtzahl der Punkte ist π/4 – umso genauer, je mehr Punkte man „geschossen“ hat.

Wahrscheinlichkeitsverteilungen

Bei diesem allereinfachsten Beispiel der Bestimmung von π wurden alle Punkte innerhalb der gewählten Grenzen als gleich wahrscheinlich gewichtet. Dies ist aber nicht immer der Fall, wesentlich öfter sind Werte um einen Mittelwert herum wahrscheinlicher als die weiter vom Mittelwert entfernten.

Beispiel Schmerzmitteldosis

Nehmen wir ein etwas willkürliches Beispiel: Ein Hersteller von Schmerzmitteln möchte vorhersagen, wie oft es zu Nebenwirkungen seiner Mittel kommt, und wie oft sie nicht wirken. Dies soll in diesem Fall direkt vom Körpergewicht abhängig sein.

Wenn eine Durchschnittsgröße der Kunden bekannt ist – in Deutschland sollen das für Männer 1,80 m und für Frauen 1,66 m sein – sowie ein durchschnittlicher BMI (Körpermasse-Index) – für Männer 27,1 kg/m² und für Frauen 25,6 kg/m² – und man außerdem davon ausgeht, dass alle diese Werte normalverteilt sind, dann könnte man mit der Übergangsgleichung BMI [kg/m²] * h²[m²] = m[kg] modellieren, mit welcher Wahrscheinlichkeit ein Patient in den zulässigen Körpergewichtsbereich für die Medikamentendosierung fällt. Auf dieser Basis könnte man z. B. entscheiden, ob es sich lohnt, getrennte Formulierungen für Männer und Frauen anzubieten.

Einerseits muss man für die tatsächliche Lösung noch mehr wissen als , vor allem über die Verteilungsfunktion (die mit ihrem Mittelwert noch nicht genügend beschrieben ist), andererseits ist dieses Problem so einfach, dass niemand dafür den Simulator anwerfen würde. Wenn aber ein Ergebnis von mehreren Variablen abhängt, die alle von unterschiedlich verteilten Variablen abhängen, dann kann man mit Hilfe der Monte-Carlo-Simulation gut vorhersagen, wie sich die möglichen Ergebnisse verteilen werden.

Weitere Beispiele

Herstellung von Dosierpumpen

Ein Hersteller von Dosierpumpen könnte durch die Einbeziehung aller Faktoren, die das Pumpvolumen beeinflussen (Fertigungstoleranzen, schwankende Betriebstemperatur, Schwankungen der Viskosität des geförderten Mediums etc.) einen Überblick darüber bekommen, mit welcher Wahrscheinlichkeit seine Geräte die geforderte Dosiergenauigkeit einhalten.

Dazu müssen ►die wichtigen Einflussgrößen, ►der mathematische Zusammenhang, mit dem sich die Einflussgröße auf das Dosierergebnis auswirkt sowie ►die Dichtefunktion der Wahrscheinlichkeitsverteilung bekannt sein. Einige der Zahlen sind historisch oder aus Messungen bekannt, andere lassen sich errechnen.

So könnte man z. B. ausrechnen, mit welcher Fertigungstoleranz man tatsächlich produzieren darf, um das Ziel einer definierten Dosiergenauigkeit für einen vorgegebenen Anteil der Pumpen zu treffen (z. B. 95% aller hergestellten Dosierpumpen werden die benötigte Dosiergenauigkeit einhalten).

Not-Aus einer Abluftreinigungsanlage

Eine katalytische Nachverbrennungsanlage darf nicht mit beliebig hohen Konzentrationen von VOC im Rohgas betrieben werden: Wird das Rohgas zu „fett“, würde sich der Katalysator so stark erhitzen, dass es zerstört werden würde. Wie wahrscheinlich ist ein solches Ereignis, hier im Beispiel einer GFK-Verarbeitung?

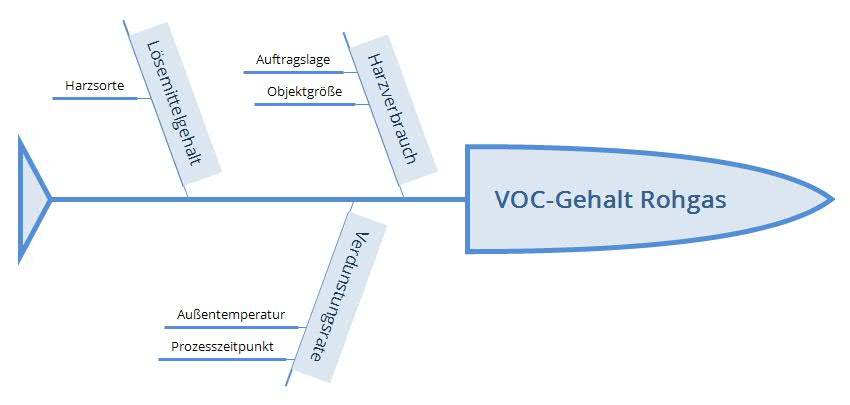
Das Diagramm zeigt stark vereinfacht die Einflussfaktoren auf den VOC-Gehalt der abgesaugten Luft an:

• Je nach Auftragslage (also der Zahl der Teile, die gleichzeitig gefertigt werden müsssen), Art und Größe der bestellten Objekte befindet sich mehr oder weniger aushärtendes Harz in der Werkhalle.
• Für unterschiedliche Behälter werden Harzsorten mit höherem oder niedrigerer VOC-Emission verwendet.
• Die Außentemperatur bestimmt die Temperatur in der Halle mit und somit auch die Verdunstungsrate.
• Auch die Größe der Objekte bestimmt ihre Temperatur – beim Polymerisieren erhitzen sich große Objekte stärker als kleine und emittieren dann auch mehr Lösungsmittel.

Für einige der Einflussgrößen lassen sich aus der Fertigungshistorie heraus Histogramme erstellen, die direkt als Wahrscheinlichkeitsverteilungen in der Simulation verwendet werden können. Wahrscheinlichkeiten für Außentemperaturen können aus historischen Wetterdaten heraus angenommen werden. Wieviel ein Teil während des Spritzens und der Härtung tatsächlich verdampft, ist entweder aus Daten der Harzhersteller bekannt, oder es müsste gemessen werden.

Wenn die Verdunstung von Lösungsmittel (in diesem Fall oft Styrol) als Funktion dieser Einflussgrößen dargestellt werden kann, kann man durch die Auswahl immer neuer zufällig generierter Datensätze eine große Zahl von Szenarien für die Rohgasbeladung simulieren. Ein typischer Wert für die Anzahl der Szenarien wäre 10.000. Die Ergebnisse lassen erkennen, in welchem Anteil dieser Szenarien die zulässige Rohgaskonzentration überschritten wird.

Die Resultate werden umso besser, je mehr man über die Wahrscheinlichkeitsverteilung seiner Variablen Bescheid weiß. So kann man zum Beispiel annehmen, große und kleine Stücke werden gleichmäßig über das Jahr verteilt gefertigt – oder man weiß, dass die großen Objekte hauptsächlich in den Monaten Januar und Februar bestellt werden, weil sie von den Landwirten im Frühjahr benötigt werden.

Im nächsten Beitrag wird es konkret

In den nächsten beiden Beiträgen werden wir uns anschauen, wie die Monte-Carlo-Simulation softwareseitig konkret umgesetzt wird. Es ist nicht überraschend, dass die meisten Tools (aber nicht alle!) auf Excel aufsetzen. Und wir werden ein konkretes Beispiel rechnen, nämlich den Chemikalienverbrauch eines Bisulfitwäschers für Formaldehyd. Dies ist ein reales Beispiel für eine Anlage, die sich nicht so verhalten hat wie erwartet.

Bis dahin noch etwas Lesestoff

• Palisade, der Hersteller der bekanntesten Software für Monte-Carlo-Simulationen @RISK, hat eine Webseite mit ausführlichen Texten zu dem Thema.
• Wie eine Monte-Carlo-Simulation mit Excel alleine zu machen ist, zeigt die entsprechende Seite auf Excel.tv.
• Für ein einfachstes Beispiel – wie jemand seine Bachelornote mit einer Monte-Carlo-Simulation vorhersagen könnte – zeigt es auch die Website der Computerzeitschrift CHIP.
• Wer lieber einen Film anschaut, kann sich von Dr. Gerard Verschuuren eine kurze Einführung über die Möglichkeiten von Excel für diese Art Simulation anschauen.