Was ist eine Adsorptionsisotherme?
Abb. 1: Adsorptionsbegriffe bildhaft erklärt
Als Adsorptionsisotherme bezeichnet man die Beziehung zwischen der freien Adsorptiv-
θA = f(pA)
oder auch mit dem Partialdruck als Anteil des Sättigungsdampfdruckes ausgedrückt:
θA = f(pA/p°A)
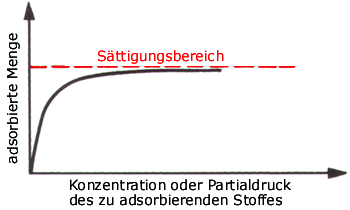
Abb. 2: Eine beispielhafte Isotherme vom Typ I
Ein Beispiel zeigt die Abbildung oben, mit der Besonderheit, dass die Adsorption einen Sättigungsbereich hat, d. h. eine Adsorbatmenge pro Gewichtsanteil Adsorbens, die nicht überschritten werden kann. Dies ist allerdings nicht für jedes Adsorbens-Adsorptiv-Paar der Fall.
Zweck einer Adsorptionsisotherme
Eine Adsorptionsisotherme kann mit zwei verschiedenen Absichten erstellt worden sein:
- Im einfacheren Fall soll einfach der gemessene Zusammenhang zwischen der Konzentration in der fluiden Phase (Gas oder Flüssigkeit) und der adsorbierten Menge mathematisch dargestellt werden. Die mathematische Form hat mit den physikalischen Hintergründen des Adsorptionsprozesses nichts zu tun, die gefitteten Parameter haben keine physikalische Bedeutung.
- Die mathematische Form der Isotherme kann aber auch als ein Modell des Adsorptionsvorganges gedacht sein. In dem Fall haben die Parameter der Isothermengleichung eine physikalische Bedeutung und verraten etwas über den Mechanismus der Adsorption.
Langmuir-Isotherme
Irving Langmuir erhielt 1932 den Nobelpreis für seine Arbeiten in der Oberflächenchemie. Er nahm zunächst an, dass ein Gasteilchen an einer Oberfläche nicht einfach elastisch abprallt, sondern dass es bindende Kräfte zwischen der Oberfläche und den beweglichen Teilchen geben müsse. Die nach ihm benannte Gleichung über den Zusammenhang zwischen Adsorptivkonzentration und adsorbierter Menge formulierte er auf Basis der folgenden Annahmen:
- Die Oberfläche des Adsorbens ist flach, gleichförmig und ohne Verwerfungen, wie eine perfekte Einkristalloberfläche.
- Die adsorbierten Moleküle sind unbeweglich und wandern nicht auf der Oberfläche herum.
- Alle Adsorptionsplätze sind energetisch äquivalent.
- Jeder Adsorptionsplatz hält nur ein Molekül, keine Doppelbelegung oder Stapelbildung.
- Die adsorbierten Moleküle beeinflussen weder den Zustand des Adsorbens, noch sich gegenseitig, noch gibt es sterische Hinderung zwischen den adsorbierten Molekülen.
Die auf diese Weise auf Basis kinetischer Überlegungen abgeleitete Isotherme hat die Form
θA = KAeq*pA/(1 + KAeq*pA) („Langmuir-Gleichung“)
θA gegen pA grafisch aufgetragen ergibt die Kurve aus Abb. 2 – die adsorbierte Menge steigt zunächst linear, dann abflachend mit dem Partialdruck in der Gasphase an und erreicht dann einen Sättigungswert, der nicht überschritten wird.
Wenn man bedenkt, dass jede der Annahmen Langmuirs extrem stark vereinfachend oder gar nicht zutreffend ist, ist es erstaunlich, dass es viele Fälle gibt, in denen die Langmuir-Gleichung die Adsorption zumindest annähernd wiedergibt. Ein Beispiel ist die Adsorption von von Wasser auf hydrophile Zeolithe vom Typ A: Hier ist das Sättigungsverhalten sehr deutlich zu beobachten.
Allerdings werden die Verhältnisse nicht wirklich genau wiedergegeben: Bei meinem Versuch, Adsorptionsdaten von Wasser auf Zeolith 3A mittels der Langmuir-Gleichung darzustellen, zeigte es sich, dass sich die Daten nicht über den ganzen Adsorptionsbereich fitten ließen. Entweder war das Modell bei niedrigen oder aber bei hohen Beladungen korrekt, nicht aber über den gesamten Bereich (siehe Abb. 3). (Die Abszisse ist hier der Taupunkt, nicht die Konzentration in der Gasphase, wofür die Isothermengleichung aber umgeformt wurde.)
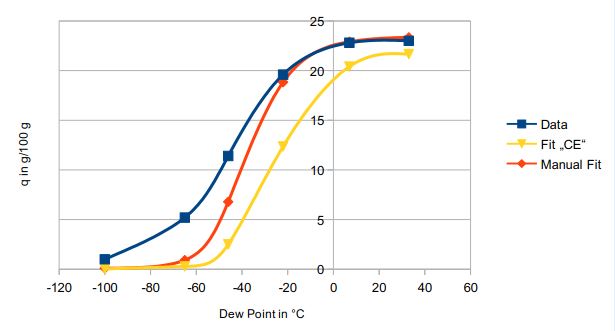
Abb. 3: Versuch der Anpassung der Langmuir-Gleichung an Adsorptionsdaten von Wasser an Zeolith 3A
Die Freundlich-Isotherme
Herbert Freundlich formulierte die nach ihm benannte Sorptions-Isothermengleichung rein empirisch, es liegt keine Theorie über die Adsorptionsvorgänge darunter:
θA = kf*cn
Hier sind schon zwei anpassbare Parameter vorhanden, kf und n, daher lässt sich die Funktion oftmals leichter an die Adsorptionsdaten anpassen. Die Funktion steigt stetig, erreicht also kein Plateau. Je nachdem n größer, kleiner oder gleich 1 ist, kann die Isotherme unterschiedliche Formen annehmen (siehe Abb. 4, die Variable für die adsorbierte Menge ist hier nicht „Theta“ θ, sondern q). Über den Sättigungsdampfdruck hinaus ist die Isotherme meist nicht gültig.
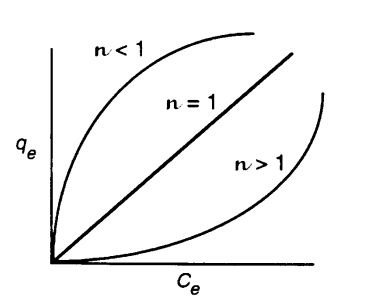
Abb. 4: Freundlich-Adsorptionsisotherme bei unterschiedlichen Werten von n [1]. Das Beispiel ist etwas irreführend, weil gleichzeitig kf verändert wurde.
- Bei Werten von n > 1 erhält man Kurven, bei denen die Adsorption erst bei höheren Konzentrationen in Gang kommt. Ein solches Verhalten zeigen Systeme, bei denen die intermolekularen Kräfte zwischen den Adsorptivteilchen stärker sind als die Kräfte, die das Adsorbat zusammenhalten, also etwa Wasser auf wasserabweisenden Oberflächen.
- Werte von n < 1 erhält man bei Systemen mit starken Adsorptionskräften.
- n = 1, also lineare Adsorptionsisothermen, werden oft nur der Einfachheit halber im Bereich niedriger Konzentrationen verwendet, weil die Berechnungen damit einfacher werden.
Adsorptionsisothermen mit mehr als zwei Parametern
Es gibt noch zahlreiche weitere Adsorptionsisothermen, die auf mechanistischen Annahmen beruhen und verschiedenen Faktoren Rechnung tragen: Etwa der energetischen Ungleichheit der Adsorptionsplätze, der Mehrschichtenbelegung, die zu mehreren Wendepunkten in der Isotherme führen kann, oder der gegenseitigen Beeinflussung von Adsorpt und Adsorbens. Bis auf eine – die BET-Isotherme – werden sie in der Praxis wenig angewendet.
Mehr dazu im November.
[1] Abbildung entnommen aus http://mimoza.marmara.edu.tr/~zehra.can/ENVE401/3.%20Adsorption%20Equilibria.pdf
Schreibe einen Kommentar