Die Gasphase – viele Wege führen zum (Partial)druck
Je nach Bedingungen und vorliegenden Daten kann man zur Abschätzung des (Partial)drucks einer Komponente in der Gasphase einen von mehreren Rechenansätzen benutzen. Die Rechenansätze basieren entweder auf vorhandenen, korrelierten Daten, wie der Verdampfungsenthalpie oder schon bekannten Wertepaaren, oder sie sind Abschätzungen, die auf den kritischen Daten basieren.
Für die Tools gilt: Sie haben mathematisch nicht viel zu tun und sind genauso gut wie die zugrundeliegende Berechnungsmethode und die Konstanten, falls welche eingetragen sind. Kontrolle mit zwei bis drei bekannten Werten genügt zur Evaluierung.
1. Die Zustandsgleichung idealer Gase – sie hat den Vorteil, einfach zu sein, und gilt annähernd entweder bei hoher Verdünnung eines Gases in der Atmosphäre (etwa wenn man Kohlenmonoxid, Argon oder andere Spurengase betrachtet) oder bei Gasen, die sich über ihrem kritischen Punkt befinden: Also gut für Stickstoff, aber ganz schlecht für Wasserdampf.
- Die Uni Erlangen bietet ein Skript mit Herleitung zu dem Thema
- Recht anschaulich ist es auch hier erklärt.
Die Zustandsgleichung idealer Gase ist so einfach, dass es dafür kaum Online-Tools gibt.
- Ein einfaches Werkzeug, mit dem man einzelne Größen nach dem Muster „1 Mol Stickstoff in einem Kubikmeter bei 300 Kelvin haben welchen Druck?“ ausrechnen kann, gibt es hier. Geschrieben hat es eine Firma für Online-Rechner.
- Noch einfacher hier, vom MIT.
- Auch recht schön gemacht: Dieser Rechner. Die Autoren lassen sich nicht recht charakterisieren, aber das ist bei einem Rechner, der nur zwei Grundrechenarten benötigt, wahrscheinlich nicht so wichtig.
2. Die Van-der-Waals-Gleichung ignoriert im Gegensatz zur idealen Gasgleichung nicht das Volumen der Teilchen und die zwischen Ihnen herrschenden Anziehungskräfte. Aus der van-der-Waals-Gleichung wurden andere, etwas besser angepasste Zustandsgleichungen gewonnen, wie etwa die Redlich-Kwong-Gleichung.
Die van-der-Waals-Gleichung hat die Form
p = (RT/(v-b) ) – a/v²
a und b sind stoffspezifische Konstanten. Die isotherme Auftragung der van-der-Waals-Gleichung macht unterhalb der kritischen Temperatur merkwürdige Schlenker, nach welchen der Druck bei Kompression abfällt, um dann wieder anzusteigen. Dieses unphysikalische Verhalten bewirkt, dass man die Kurve im Zweiphasengebiet sozusagen ignorieren, bzw. durch eine Maxwell-Gerade ersetzen muss. Eine verständliche Darstellung der van-der-Waals-Gleichung ist auf den Seiten der Uni Frankfurt zu sehen.
Hier ein Vergleich zwischen den beiden Zustandsgleichungen, zunächst in einem Fall, in dem die ideale Gasgleichung gut geeignet sein sollte: Isothermen von Stickstoff bei Raumtemperatur und einer Kompression zwischen ca. 1 und 10 bar.
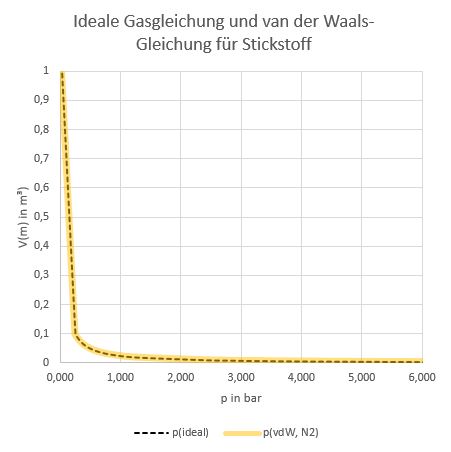
Isothermenplot für Stickstoff bei 298 K
Hier sieht man, dass man nichts sieht – bei Stickstoff, dessen kritische Temperatur bei 126 K liegt, kann die ideale Gasgleichung bei Raumtemperatur ebenso angewendet werden wie die van der Waals-Gleichung. Bei Chlor sieht man im selben Auftragungsbereich zwar ebenfalls keine Unterschiede, aber Chlor verflüssigt sich bei 6,7 bar. Ab dort weichen die Isothermen signifikant voneinander ab, aber der Verlauf macht physikalisch keinen Sinn mehr. Bei dieser Form der Auftragung ist das allerdings an nichts zu erkennen ist, bei 6,7 bar handelt sich um einen Literaturwert.
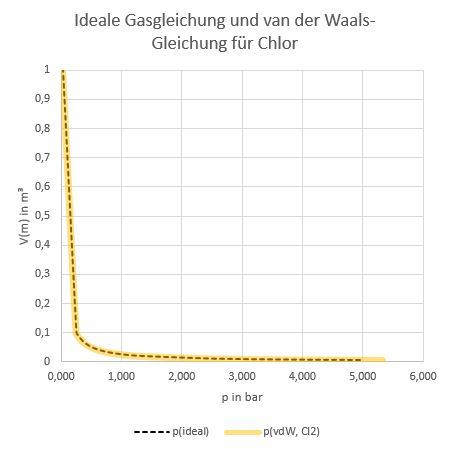
Isothermenplot bei 298 K
Zweiphasensysteme
Neben den einfachen Druck-Temperatur-Volumenbeziehungen gibt es oft auch Sättigungsdampfdrücke über flüssigen Phasen zu berechnen. Will man nicht eine der neueren, für Gase und Flüssigkeiten geeigneten Zustandsgleichungen benutzen [1], muss man auf einen der einfacheren Ansätze zur Berechnung der Zweiphasengleichgewichte ausweichen.
3. Die Clausius-Clapeyron’sche Gleichung lautet in ihrer vollständigen Form
dp/dT = ΔHv/ΔVvT mit
- ΔHv = Verdampfungsenthalpie und
- ΔVv = molare Volumenänderung
Mit einer Reihe von Vereinfachungen [2] und Integration erhält man
ln(p2/p1) = (ΔHv/R) * (1/T1 – 1/T2)
mit der universellen Gaskonstante R (8,3143 J/K mol)
Für Auftragungen vereinfacht man das zu
ln(p) ~ 1/T
Man kann somit aus zwei Wertepaaren eine Dampfdruckurve interpolieren. Einen Wert hat man schon einmal durch die Angabe des Siedepunktes – p ist dann 101.300 Pa – und einem angegebenen Dampfdruck, etwa aus einem Sicherheitsdatenblatt. Genau auf diesem Prinzip basieren Rechner wie z. B. das Excel-Blatt „Dampfdruckinterpolation„.
Andere Rechner, wie etwa die Shareware „Dampfdruck 3.0„, benutzen auf kritischen Daten beruhende Abschätzungen, die oberhalb des Siedepunktes meistens genauer sind als Clausius-Clapeyron, unterhalb aber bis zu 10% Fehler aufweisen können.
4. Antoine-Gleichung – diese ist von der Clausius-Clapeyron’schen Gleichung abgeleitet und leidet demgemäß an den gleichen Beschränkungen. Sie hat die Form
log10(p) = A – B/(C+T)
Das ehrwürdige Alter dieser Gleichung zeigt sich darin, dass der Druck p noch oft in torr und die Temperatur in °C angegeben werden müssen, damit die stoffspezifischen Konstanten A, B und C richtig sind. Da die Antoine-Gleichung oberhalb des Siedepunktes (bei Normaldruck) nicht mehr gut passt, wird zwischen Siedepunkt und kritischem Punkt ein zweiter Satz experimentell gewonnener Konstanten A, B und C verwendet – mit der Folge, dass die Dampfdruckkurve am Siedepunkt einen Bruch hat. Wikipedia hat einige Beispiele dazu.
5. Weitere Rechenmethoden gehen von den kritischen Daten aus, oder auch von der Molekularstruktur. Sie sind nützlich, wenn keine weiteren Stoffdaten zur Verfügung stehen, können aber mit der Vorhersage auch ziemlich danebenliegen.
- Artikel über eine Berechnungsmethode basierend auf Molekülfragmenten. Enthalten ist jedoch auch ein Vergleich mit anderen Berechnungsmethoden.
- Dr. Hiroshi Yamamoto stellt eine weitere Berechnungsmethode, sowie eine Übersicht über die wichtigsten Methoden vor. Klick auf die Links führt zu Online-Tools, die allerdings nicht in jedem Browser laufen (uralt-Java…)
- Der Programmteil MPBPVP der EPI-Suite benutzt gleichzeitig mehrere Modelle und mittelt die Ergebnisse, zeigt aber im Protokoll, was die Einzelergebnisse gewesen sind.
- Noch ein Eigenschaftenrechner, der neben dem Dampfdruck noch eine Reihe anderer Parameter ausgibt (allerdings nur für eine Reihe voreingestellter Verbindungen). Hier kann man zu jedem errechneten Wert die Berechnungsdetails nachschlagen. Ethanol siedet schon mal bei 78 °C, ganz falsch kann die Geschichte also nicht sein.
Nur sollte man bedenken, wie falsch schon ein „fast richtig“ sein kann…
[1] wie etwa Soave-Redlich-Kwong, Peng-Robinson oder Benedict-Webb-Rubin-Starling (BWRS). Diese haben deutlich mehr Parameter, die BWRS-Gleichung hat elf.
[2] die Verdampfungsenthalpie sei über den betrachteten Temperaturbereich konstant, die molare Volumenänderung sei gleich der Volumenänderung des Gases, die vergleichsweise kleine Volumenänderung der Flüssigkeit wird vernachlässigt, und für das Gas gilt – da es verdünnt ist – die ideale Gasgleichung
[…] einfachsten werden Gasdichten durch das Ideale Gasgesetz berechnet, nach dem die Dichte eines (nicht allzu komprimierten und im Idealfall überkritischen) […]