Wie schon im Teil I dieses Beitrages erwähnt, werden in der Praxis kaum andere Adsorptionsisothermen verwendet als die von Langmuir, Freundlich und Geradengleichungen (manchmal fälschlich als „Henry“-Isotherme bezeichnet). Andere Isothermen, denen man in der Praxis noch begegnet, sind
- die BET-Isotherme, die vor allem zur Bestimmung von Adsorbensoberflächen benutzt wird
- die Dubinin-Radushkevich-Isotherme oder eine ihrer zahlreichen Abwandlungen, die vor allem die energetische Verteilung der Adsorptionsplätze gut abbilden kann.
Es gibt daneben noch zahlreiche weitere Ansätze für Isothermengleichungen mit ebenso vielen Abwandlungen und Weiterentwicklungen, oft für spezielle Anwendungen konzipiert, wie etwa
- Fumkins und Flory-Huggins (für die Adsorption einer Mischung unterschiedlich großer Moleküle auf homogene Oberflächen und die Berücksichtigung von Adsorpt-Adsorpt-Wechselwirkungen, siehe z. B. [1])
- Hill (Beschreibung des Adsorbates als ein zweidimensionales Gas, welches von einem Kraftfeld auf der Oberfläche gehalten wird, unter Berücksichtigung der lateralen Wechselwirkungen der Adsorptmoleküle untereinander [2])
- Sips und Toth, beides Weiterentwicklungen und Verbesserungen der Langmuir-Isotherme, die die Anpassung an experimentelle Daten verbessern sollen.
Eine gute Übersicht über eine Vielzahl von Isothermengleichungen gibt z. B. [3].
BET-Isothermen
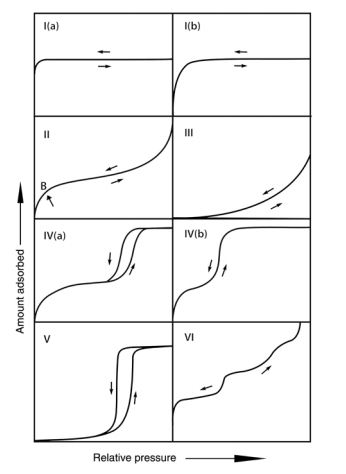
Klassifizierung von Physisorptionsisothermen nach IUPAC, aus [5]
Die BET-Isotherme beschreibt die Verhältnisse am besten bei niedrigen bis mittleren Dampfdrücken, etwa zwischen 5 und 30% des Sättigungsdampfdruckes. Bei niedrigeren Gasphasenkonzentrationen machen sich die Inhomogenitäten der Oberfläche, die das Modell nicht berücksichtigt, zu stark bemerkbar, während bei zu hohen Gasphasenkonzentrationen zu viele Schichten ausgebildet werden. Damit werden Unebenheiten – etwa Risse und Versetzungen – der Oberfläche aufgefüllt, die dadurch verkleinert wird, statt gleich groß zu bleiben.
Hauptanwendung: Bestimmung der inneren Oberfläche
Die BET-Isotherme wird eingesetzt, um die innere Oberfläche von Adsorbenzien zu bestimmen. Man braucht dazu eine Annahme über die Fläche, die ein einzelnes Adsorptmolekül bedeckt, was eben nur eine Annahme ist. Außerdem wird die Methode auch für mikroporöse Materialien, etwa Zeolithe, verwendet, die genau genommen keine innere Oberfläche in der Form, wie sie das Modell vorsieht, haben.
Liest man daher Angaben wie „BET = 981 m²/g“, so dienen solche Zahlen nur dazu, zwei Proben gleichartiger Adsorbenzien miteinander zu vergleichen, und sind nicht absolut zu sehen. Trotzdem ist die Angabe sehr hilfreich, um etwa
- die ansonsten ähnlichen Produkte zweier Hersteller/Chargen zu vergleichen
- gebrauchtes Adsorbens mit dem Neuzustand zu vergleichen.
Charakteristische Kurven nach Dubinin-Radushkevich (DR)
Die DR-Isotherme wurde ursprünglich als semiempirische Anwendung der Potenzialtheorie nach Polanyi auf die Adsorption entwickelt und eignet sich besonders für die Adsorption an mikroporösen Adsorbenzien, wie Zeolith und Aktivkohle, bei mittleren Partialdrücken [8]. Ihre Besonderheit ist, dass durch die gewählte Darstellung der Einfluss der Temperatur verschwindet und alle Isothermen auf eine einzige „charakteristische Kurve“ zusammenfallen. Das Adsorptionspotenzial Ax (mit der Einheit J/mol) wird dargestellt als Funktion des adsorbierten Volumens.
Ax = R T * ln(p°/px)
R = Allgemeine Gaskonstante
T = thermodynamische Temperatur
p° = Sättigungsdampfdruck des Adsorptives
px = Gleichgewichtsdampfdruck über dem Adsorbat bei der Beladung x
Wie die charakteristische Kurve aussehen kann, zeigt die folgende Abbildung (aus [9]):
Was kann man aus der charakteristischen Kurve erkennen?
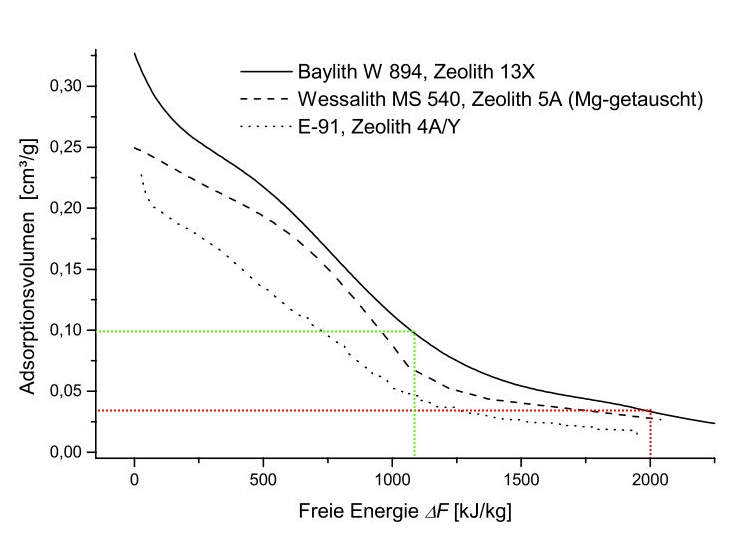
Charakteristische Kurven von Wasserdampf auf verschiedenen Zeolithen, aus [9], Ablesungen nachträglich eingezeichnet.
- Wenn das Adsorptionspotenzial (welches gleichbedeutend ist mit der Freien Energie) gleich Null ist, ist die maximale Beladung erreicht. Diese ist für Baylith W894 etwa 0,325 cm³/g, für E-91 0,225 cm³/g. Die Volumenangaben beziehen sich auf das Volumen der adsorbierten Phase, die ähnliche, aber nicht identische Eigenschaften wie die flüssige Phase hat.
- Wenn bei W 894 das Adsorptionsvolumen von ca. 0,0375 cm³/g auf 0,1 cm³/g gesteigert wird (Ablesung Ordinate), werden ca. 900 kJ/kg Adsorbens frei. Je flacher die charakteristische Kurve in einem Bereich verläuft, desto mehr Energie wird bei der Adsorption einer vorgegebenen Menge Adsorptiv frei.
- Wenig beladene Zeolithe (rechter Bereich der Kurve) setzen beim Adsorbieren mehr Energie frei als bereits vorbeladene. D. h. die Adsorption ein und der selben Menge Adsorptiv setzt mal mehr, mal weniger Energie frei, je nach Anfangszustand des Adsorbens.
Auch wenn man aus der charakteristischen Kurve nicht direkt auf die adsorbierte Menge schließen kann (dazu müsste man die Dichte der adsorbierten Phase kennen, die nicht direkt messbar ist), ist die charakteristische Kurve doch sehr nützlich für den Vergleich verschiedener Adsorbenzien unter energetischen Gesichtspunkten.
[1] „Generalized Flory–Huggins isotherms for adsorption from solution„. Panaghiotis Nikitas, J. Chem. Soc., Faraday Trans. 1, 1984,80, 3315-3329
[2] Darstellung nach „Equilibria and Dynamics of Gas Adsorption on Heterogeneous Solid Surfaces„, eBook ISBN: 9780080531199
[3] „Insights into the modeling of adsorption isotherm systems.“ K.Y. Foo, B.H. Hameed, Chemical Engineering Journal 156 (2010) 2–10
[4] Brunauer, S., Emmett, P. H. & Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 60, 309-319, 1938
[5] Matthias Thommes, Katsumi Kaneko, Alexander V. Neimark, James P. Olivier, Francisco Rodriguez-Reinoso, Jean Rouquerol and Kenneth S. W. Sing. „Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report)„. Pure Appl. Chem. 2015; 87(9-10): 1051–1069
[6] „Adsorption Equilibria“, gefunden unter http://mimoza.marmara.edu.tr/~zehra.can/ENVE401/3.%20Adsorption%20Equilibria.pdf,
[7] „Derivation of the BET and Langmuir Isotherms„, Skript der Uni Ulm, 2011.
[8] Nguyen, C., & Do, D. . (2001). „The Dubinin–Radushkevich equation and the underlying microscopic adsorption description„. Carbon, 39(9), 1327–1336. Die Arbeit enthält einige mathematische Fehler im einführenden Teil.
[9] Hauer, A., & Auracher, H. (2002).“Beurteilung fester Adsorbentien in offenen Sorptionssystemen für energetische Anwendungen.„Fakultät III Prozesswissenschaften. TU Berlin, Berlin.
Schreibe einen Kommentar