Das Phänomen der Knudsen-Strömung wurde 1907 – 1908 von dem dänischen Physiker Martin Knudsen untersucht (nicht zu verwechseln mit dem Fußballspieler Martin Knudsen). Die ursprüngliche Versuchsanordnung war eine Zelle, in deren Wand ein kleines Loch war und die eine flüchtige Probe enthielt ( eine Abbildung ist z. B. im Zusammenhang der Beschreibung eines Knudsen-Effusions-Massenspektrometers zu sehen). Bei ausreichend hohem Druck strömte das eingeschlossene Gas wie erwartet aus der sog. Knudsen-Zelle, der Fluss proportional zur Druckdifferenz, oder wenn keine Druckdifferenz vorliegt, nach den Gesetzen der Diffusion in Richtung des Konzentrationsgradienten. Bei sehr kleinen Drücken jedoch ändern sich die Verhältnisse.
eine Abbildung ist z. B. im Zusammenhang der Beschreibung eines Knudsen-Effusions-Massenspektrometers zu sehen). Bei ausreichend hohem Druck strömte das eingeschlossene Gas wie erwartet aus der sog. Knudsen-Zelle, der Fluss proportional zur Druckdifferenz, oder wenn keine Druckdifferenz vorliegt, nach den Gesetzen der Diffusion in Richtung des Konzentrationsgradienten. Bei sehr kleinen Drücken jedoch ändern sich die Verhältnisse.
Ursache dafür ist das Verhältnis von mittlerer freier Weglänge der Gasmoleküle zu der zur Verfügung stehenden „Flugstrecke“, also den Dimensionen des Behälters. Wird der Druck sehr gering (also die Moleküle weit verteilt) oder das Behältnis sehr klein (wie in den Poren poröser Materialien), dann werden die Stöße der Moleküle untereinander deutlich seltener als die Stöße der Moleküle mit der Wand, was die Transportvorgänge entschieden beeinflusst.
Der Einfluss der Dimensionen
Bei 0 °C und 1 bar haben Gase die folgenden mittleren freien Weglängen und Stoßzahlen [1]:
| Gas | Stoßzahl Z | mittlere freie Weglänge λ |
| s-1 | cm | |
| N2 | 7,58 * 109 | 0,6 * 10-5 |
| CO2 | 9,13 * 109 | 0,397 * 10-5 |
| H2 | 15,14 * 109 | 1,123 * 10-5 |
Die typische mittlere freie Weglänge liegt also um 0,1 µm. Je nach Dimension des umgebenden Gefäßes stoßen die Teilchen häufiger aneinander oder häufiger an die Wand, wodurch sich unterschiedliche Strömungsverhältnisse einstellen:
- Bei den Verhältnissen der Kontinuumsströmung (hohe Drücke, große Gefäße) ist der Raum gleichmäßig mit Gasmolekülen ausgefüllt, das Gas bewegt sich als ein viskoses Ganzes, die einzelnen Moleküle bewegen sich bevorzugt in Richtung der „Bulkströmung“. Die Viskosität ist eine der Einflussgrößen für den Stofftransport.
- Bei den Verhältnissen der Knudsen-Strömung (niedrige Drücke, kleine Gefäße) wechselwirken die Moleküle nicht mehr miteinander, sondern nur noch mit den Wandungen. Es gibt keine eigentliche Strömung mehr, bzw. zwischen Strömung und Diffusion kann kein Unterschied mehr gemacht werden. Nur noch die Wahrscheinlichkeit, mit der sich ein Molekül in die richtige Richtung bewegt, bestimmt seine Transportgeschwindigkeit. Die Viskosität eines Gases spielt keine Rolle mehr (da die Moleküle nicht mehr miteinander wechselwirken, gibt es die Effekte der Viskosität nicht mehr), dafür geht das Molekulargewicht ein.
Diese Verhältnisse (einschließlich der Formeln für die Strömung) sind auf der Website von Lazzero erklärt (die Firma nutzt die Strömungseffekte als Funktionsprinzip für Lecksuchgeräte). Die folgende Abbildung illustriert die Verhältnisse:
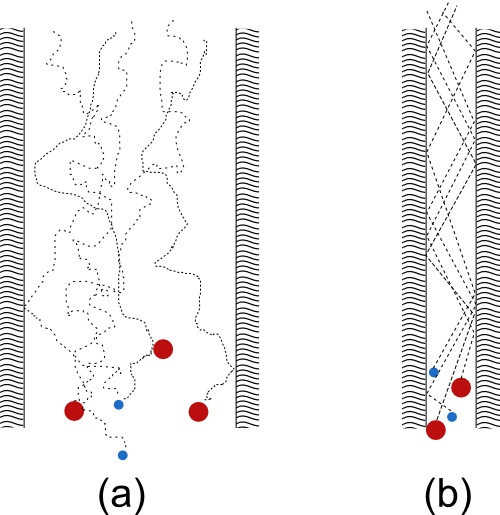
Vergleich zwischen viskoser (a) und Knudsenströmung (b).
- (a) stellt die gewöhnliche viskose Strömung dar, bei der der gemischte Gasstrom einheitlich durch das Rohr strömt und in gleichem Mischungsverhältnis am anderen Ende ankommt. Die Druckdifferenz geht ein mit p1² – p2².
- (b) zeigt die Verhältnisse der Knudsen-Strömung. Hier bewegen sich die leichteren Moleküle schneller als die schwereren, und zwar im Verhältnis der Molekulargewichte. Die Druckdifferenz geht ein mit p1 – p2.
- Es gibt einen Zwischenbereich, in dem sich beide Effekte überlappen.
Knudsen-Zahl
Welche Verhältnisse vorherrschen, wird durch die dimensionslose Knudsen-Zahl Kn angezeigt. Sie ist definiert als das Verhältnis von mittlerer freier Weglänge λ zur charakteristischen Länge L des Behälters: Kn = λ/L
- Kn < 0,01: Viskose Strömung
- Kn ≥ 2: Knudsen-Strömung (engl. „free molecular flow“)
- Bei den dazwischenliegenden Werten findet man Übergangsformen, für die sich der Stofftransport nur schwer modellieren lässt.
Eine Schwierigkeit kommt durch den Begriff „charakteristische Länge“ hinzu, die sich oft nur experimentell bestimmen lässt. Bei einfach geformten Behältern (z. B. zylindrischen Poren) ist L gleich dem Durchmesser, bei kompliziert geformten Hohlräumen stimmt das oft nur näherungsweise [2]. Bei V-förmigen Poren wäre der Effekt bei der Effusion überhaupt nicht zu beobachten, bei flaschenförmigen Poren stärker als erwartet.
Zeolithe
Wie sehen die Verhältnisse in Zeolithen aus? Welche Strömungsverhältnisse trifft man im Transportporensystem und den Mikroporen an? Zu diesem Zweck habe ich die Knudsen-Zahl als Funktion von Druck und Temperatur einmal geplottet, und zwar für Methan in 0,1 µm-Poren. Während für die eigentlichen Nanoporen des Zeolithen gilt, dass dort Adsorptions- und Desorptionsvorgänge das Bild beherrschen, kann es im Transportporensystem, das je nach Hersteller des Zeolithpellets Durchmesser von 0,1 µm aufweist [3], zu Knudsen-Strömung kommen. Der Plot zeigt, dass man sich, zumindest für Methan, durchweg im Übergangsbereich befindet.
Quellen:
[1] Kleine Enzyklopädie „Struktur der Materie“, Ch. Weißmantel et al., Leipzig 1982
[2] http://www.fml.ethz.ch/slidescheming/handouts/H3_Transport.pdf
[3] Zitiert nach K. Sattler, „Thermische Trennverfahren“, ISBN 3-527-26727-1, Tab. 4.7
Schreibe einen Kommentar